MATH CONCEPTS
Please click on the links for explanations and videos
Prime and Composite Numbers
🔢 Prime and Composite Numbers
Prime Numbers
A prime number has exactly two factors — 1 and itself.
That means it can only be divided evenly by 1 and the number itself.
🟢 Examples: 2, 3, 5, 7, 11, 13, 17
👉 2 is the only even prime number.
Composite Numbers
A composite number has more than two factors — it can be divided
evenly by other numbers besides 1 and itself.
🟣 Examples: 4 (1×4, 2×2), 6 (1×6, 2×3), 8, 9, 10
Special Note:
-
The number 1 is neither prime nor composite, because it has only one factor (itself).
What are prime and composite numbers?
Prime and Composite Worksheet 1
FACTORS
🔢 What Are Factors?
Factors are the numbers you can multiply together to get another number.
They show what evenly divides into that number — with no remainder.
Example:
The factors of 12 are 1, 2, 3, 4, 6, and 12 because:
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
So, 12 has six factors.
Tips:
-
Every number has at least two factors: 1 and itself.
-
Numbers with only two factors (1 and itself) are called prime numbers.
-
Numbers with more than two factors are called composite numbers.
Extra Practice Factor Worksheets 1
Extra Practice Factor Worksheets 2
MULTIPLES
🔢 What Are Multiples?
Multiples are the numbers you get when you multiply a number by whole numbers (1, 2, 3, 4, …).
In other words, a multiple is a number found in that number’s times table.
Example:
The multiples of 4 are:
4, 8, 12, 16, 20, 24, 28, 32, …
(because 4×1=4, 4×2=8, 4×3=12, etc.)
Key Ideas:
-
Every number is a multiple of itself.
-
Multiples go on forever.
-
The smallest multiple two numbers share is called the least common
multiple (LCM).
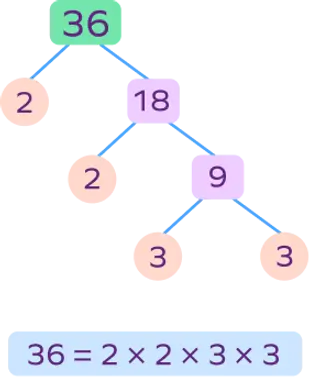
PRIME FACTOR TREES
🌳 Prime Factor Trees
A prime factor tree is a diagram that helps you break a number down into its prime factors — the prime numbers that multiply together to make the original number.
Steps:
-
Start with a number (e.g., 24).
-
Break it into two factors that multiply to make that number.
24 → 4 × 6
-
Keep breaking down each factor until every branch ends in a prime number.
4 → 2 × 2
6 → 2 × 3 -
Circle the prime numbers (the ends of the branches).
-
Write the number as a product of those primes.
✅ Prime factorization: 24 = 2 × 2 × 2 × 3
Or written with exponents: 2³ × 3
Why It’s Useful
-
Helps simplify fractions
-
Finds greatest common factors (GCF) and least common multiples (LCM)
-
Builds number sense and links multiplication/division concepts
LEAST COMMON MULTIPLE (LCM)
🔢 Least Common Multiple (LCM)
The Least Common Multiple is the smallest number that is a multiple of two or more numbers.
It’s the first (lowest) number that appears in both numbers’ multiplication tables.
🧮 Example 1:
Find the LCM of 4 and 6
Multiples of 4 → 4, 8, 12, 16, 20, 24, …
Multiples of 6 → 6, 12, 18, 24, 30, …
✅ The common multiples are 12, 24, 36…
👉 The least common multiple is 12.
⚙️ Prime Factor Method (Another Way)
-
Write each number’s prime factors:
-
4 = 2 × 2
-
6 = 2 × 3
-
-
Multiply each prime factor the greatest number of times it appears:
-
2 × 2 × 3 = 12
-
✅ LCM = 12
💡 Why It’s Useful
-
Finding a common denominator for fractions
-
Solving problems with repeating patterns or timed events
-
Working with ratios and equivalent fractions
GREATEST COMMON FACTOR (GCF)
🔢 Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) is the largest number that divides evenly into two or more numbers.
It’s also called the Greatest Common Divisor (GCD).
🧮 Example 1:
Find the GCF of 12 and 18
Factors of 12 → 1, 2, 3, 4, 6, 12
Factors of 18 → 1, 2, 3, 6, 9, 18
✅ The common factors are 1, 2, 3, and 6.
👉 The greatest common factor is 6.
⚙️ Prime Factor Method (Another Way)
-
Write each number as a product of prime factors:
-
12 = 2 × 2 × 3
-
18 = 2 × 3 × 3
-
-
Identify the primes they have in common:
-
Common = 2 × 3
✅ GCF = 6
-
💡 Why It’s Useful
-
Simplifying fractions
-
Reducing ratios to simplest form
-
Solving problems involving equal grouping or sharing
Explanation Video Using the List Method
COMPARING AND ORDERING DECIMALS
💯 Comparing and Ordering Decimals
Decimals show parts of a whole — and just like whole numbers, we can compare them to see which is greater or smaller, and order them from least to greatest (or vice versa).
🧮 Steps to Compare Decimals
-
Line up the decimals vertically by the decimal point.
-
Add zeros if needed so they have the same number of decimal places.
-
Compare digits from left to right — starting with the tenths, then hundredths, then thousandths.
-
The first place value that’s different decides which number is greater.
✏️ Example:
Compare 0.56 and 0.5
Line them up:
0.56
0.50
Compare tenths → both have 5
Compare hundredths → 6 > 0
✅ So, 0.56 is greater than 0.5
📊 Ordering Example:
Order 0.3, 0.45, 0.29, 0.305 from least to greatest.
Add zeros: 0.30, 0.45, 0.29, 0.305
Now compare digit by digit:
0.29 → 0.30 → 0.305 → 0.45
✅ Order: 0.29, 0.30, 0.305, 0.45
💡 Tips
-
Think of decimals like money!
-
$0.50 = 50¢, $0.56 = 56¢ → 56¢ is greater.
-
-
Use a place value chart (tenths, hundredths, thousandths).
-
If numbers have the same digits, they are equal (e.g., 0.5 = 0.50).
Comparing Decimals Extra Worksheet
ADDING AND SUBTRACTING DECIMALS
➕➖ Adding and Subtracting Decimals
Decimals work just like whole numbers — you just have to line up the decimal points so the place values (ones, tenths, hundredths, etc.) match.
🧮 Steps:
-
Line up the decimal points vertically.
-
Add zeros to make sure each number has the same number of decimal places.
-
Add or subtract just like whole numbers.
-
Bring the decimal point straight down into your answer.
✏️ Example 1 – Adding
2.35
+1.70
4.05
✅ The sum is 4.05
✏️ Example 2 – Subtracting
5.80
– 2.46
3.34
✅ The difference is 3.34
💡 Tips
-
Always line up the decimals — that’s the most common mistake!
-
Use place value words to check:
-
0.5 is five-tenths, 0.05 is five-hundredths (very different!).
-
-
You can estimate first to see if your answer makes sense.
Adding Decimals Extra Worksheet
MULTIPLYING DECIMALS
In multiplying decimal numbers, we look at the numbers without there being a decimal. For example 2.3x1.2 would be 23x12. You would move your decimal to the left in the product depending on how many digits are after the decimals in your question.
AREA MODEL METHOD
Multiplying Decimals Extra Worksheet
STANDARD ALGORITHM METHOD
✖️ Multiplying Decimals
When you multiply decimals, you multiply them like whole numbers first, then place the decimal in your answer.
🧮 Steps:
-
Ignore the decimals and multiply like whole numbers.
-
Count the total number of decimal places in both factors.
-
Place the decimal in the product so it has the same number of decimal places as the total you counted.
✏️ Example 1:
0.3 × 0.4
Step 1: 3 × 4 = 12
Step 2: Each factor has one decimal place (two total).
Step 3: Put the decimal two places from the right → 0.12
✅ 0.3 × 0.4 = 0.12
✏️ Example 2:
2.5 × 0.6
Step 1: 25 × 6 = 150
Step 2: Two total decimal places (one in each factor).
Step 3: 1.50 → 1.5
✅ 2.5 × 0.6 = 1.5
💡 Tips
-
Estimate first to check:
2.5 × 0.6 is a bit more than half of 2.5 → about 1.5 ✅ -
The answer to multiplying decimals is often smaller than the original numbers (if both are less than 1).
-
You don’t need to line up the decimal points when multiplying!
Multiplying decimals Video
Multiplying Decimals (Decimals by 1 whole number) Extra Worksheet
Multiplying Decimals (2 Decimals by 2 decimals) Extra Worksheet
DIVIDING DECIMALS (2 Methods)
🧮 Case 1: Dividing a Decimal by a Whole Number
Example: 6.4 ÷ 4
-
Set up the division: 4 ⟌ 6.4
-
Bring the decimal point straight up into your answer.
-
Divide like normal:
-
4 goes into 6 once → 1
-
1 × 4 = 4 → subtract → 2
-
Bring down the 4 → 24
-
4 goes into 24 six times → 6
✅ Answer: 1.6
-
🧮 Case 2: Dividing a Decimal by a Decimal
Example: 3.6 ÷ 0.6
-
Move the decimal in the divisor (0.6) to make it a whole number → move it one place right.
-
Move the decimal in the dividend (3.6) the same number of places → becomes 36 ÷ 6.
-
Divide like normal: 36 ÷ 6 = 6
✅ Answer: 6
💡 Tips
-
Always move the decimal in both numbers the same amount when dividing by a decimal.
-
Estimate first to check if your answer makes sense.
-
If needed, add zeros to the dividend (e.g., 12.3 → 12.30 → 12.300) to keep dividing evenly.
✏️ Example 3:
4.8 ÷ 0.2
Move both decimals one place → 48 ÷ 2 = 24
✅ Answer: 24
LONG DIVISION
Dividing whole numbers by decimals
Dividing whole numbers by decimals Video
Dividing decimals by decimals
Dividing decimals by decimals Video
REPEATED SUBTRACTION
Use the same decimal rules for as above but use the repeated subtraction method.
INTEGERS
WHAT IS AN INTEGER?
🔢 Integers
Integers are whole numbers and their opposites.
That means they include:
✅ Positive numbers (1, 2, 3, …)
✅ Negative numbers (–1, –2, –3, …)
✅ And zero (0)
📊 Examples of Integers
…, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, …
Integers go forever in both directions on the number line.
⚖️ How Integers Work
-
Positive integers are greater than zero (above sea level, money you have).
-
Negative integers are less than zero (below sea level, money you owe).
-
Zero is neutral — it’s neither positive nor negative.
💡 Real-Life Examples
-
Temperature: –10°C is colder than 0°C
-
Money: –$5 means you owe $5
-
Elevation: –20 m is below sea level
-
Game points: losing 3 points = –3
🧮 Tips
-
On a number line, numbers increase to the right and decrease to the left.
-
The opposite of a number is the same distance from zero in the other direction (e.g., opposite of +4 is –4).
What is an integer? Explanation Video
COMPARING AND ORDERING INTEGERS
🔢 Comparing and Ordering Integers
Integers can be positive, negative, or zero.
To compare them, think about their position on the number line:
👉 Numbers to the right are greater, and numbers to the left are smaller.
📊 Example:
–3 and 2
On a number line, –3 is to the left of 2.
✅ So, –3 < 2 (“–3 is less than 2”).
Another Example:
–5 and –1
Even though 5 is bigger than 1, –5 is smaller
because it’s farther left.
✅ So, –5 < –1
🧮 Ordering Integers
To order integers:
-
Draw or picture a number line.
-
Remember: numbers increase as you move right.
-
Arrange them from least to greatest (left to right) or greatest to least (right to left).
Example:
Order –4, 3, –2, 0, 1 from least to greatest →
✅ –4, –2, 0, 1, 3
💡 Tips
-
Negative numbers are always less than zero.
-
Zero is between the positives and negatives.
-
The farther left a number is, the smaller it is.
-
Use inequality symbols:
-
< means “less than”
-
> means “greater than”
-
Example:
–7 < –2 < 0 < 5
Comparing integers explanation video
Ordering integers explanation video
ADDING INTEGERS
🔢 Adding Integers with Models
We can use integer chips or number lines to help us understand how positive and negative numbers combine.
🟡 1. Integer Chip Model
Yellow chip = +1 (positive)
Red chip = –1 (negative)
When you put a yellow and a red chip together, they make a zero pair (they cancel each other out).
✏️ Example 1: (+3) + (–2)
Start with 3 yellow chips and 2 red chips.
-
2 yellow and 2 red make zero pairs.
-
You have 1 yellow chip left.
✅ Answer: +1
✏️ Example 2: (–4) + (+2)
Start with 4 red chips (–4) and add 2 yellow chips (+2).
-
2 red and 2 yellow cancel out → 2 red remain.
✅ Answer: –2
✏️ Example 3: (–3) + (–2)
Start with 3 red chips, add 2 more red chips.
-
Combine → 5 red chips.
✅ Answer: –5
💡 Rule You’ll Notice
-
Same signs → add the numbers and keep the sign.
-
(–3) + (–2) = –5
-
(+4) + (+2) = +6
-
-
Different signs → subtract the smaller from the larger and keep the sign of the larger number.
-
(–4) + (+2) = –2
-
(+5) + (–3) = +2
-
📏 2. Number Line Model
-
Start at the first number on the number line.
-
Move right for positive numbers, left for negative numbers.
Example: (+2) + (–5)
Start at +2 → move 5 left → land on –3
✅ Answer: –3
Adding integer with models explanation video
SUBTRACTING INTEGERS
🔢 Subtracting Integers with Models
Subtracting integers can feel tricky at first — but using models makes it visual and easy to understand!
You can use integer chips (positive and negative counters) or a number line.
🟡 1. Integer Chip Model
Yellow chip = +1 (positive)
Red chip = –1 (negative)
A zero pair is one yellow and one red chip (they cancel out).
✏️ Example 1: (+5) – (+3)
Start with 5 yellow chips.
Now take away 3 yellow chips.
✅ You have 2 yellow chips left → +2
✏️ Example 2: (+3) – (–2)
Start with 3 yellow chips.
You need to take away 2 red chips, but you don’t have any!
👉 So, add zero pairs (1 yellow + 1 red) until you have red chips to remove.
Now remove 2 red chips — you’ll have 5 yellow chips left.
✅ Answer: +5
✏️ Example 3: (–4) – (+2)
Start with 4 red chips.
Take away 2 yellow chips — but you don’t have any yellow!
👉 Add zero pairs (red + yellow).
Remove 2 yellow chips → now you have 6 red chips left.
✅ Answer: –6
💡 Rule You’ll Notice
-
Subtracting a positive moves you left on the number line (or removes yellow chips).
-
Subtracting a negative moves you right (or removes red chips).
✅ Subtracting a negative is the same as adding a positive.
Example: 3 – (–2) = 3 + 2 = 5
📏 2. Number Line Model
-
Start at the first number.
-
If subtracting a positive, move left.
-
If subtracting a negative, move right.
Example: (–2) – (–4)
Start at –2 → subtracting a negative means move 4 right → land on +2
✅ Answer: +2
Subtracting integer with models
Subtracting integer with models explanation video
Addition and Subtraction Maze Extra Worksheet
Addition and Subtraction Riddle Extra Worksheet
MULTIPLYING INTEGERS
✖️ Multiplying Integers with Models
Multiplying integers means combining equal groups — and the signs tell us which direction or type of group we have.
We can use number lines or two-color counters (integer chips) to model this.
🧮 1. The Rules of Multiplying Integers
Sign PatternExampleResult
(+) × (+)3 × 2 = 6Positive
(+) × (–)3 × –2 = –6Negative
(–) × (+)–3 × 2 = –6Negative
(–) × (–)–3 × –2 = +6Positive
💡 Same signs = positive
💡 Different signs = negative
🟡 2. Integer Chip Model (Visual Thinking)
-
Yellow chip = +1
-
Red chip = –1
✏️ Example 1: (+2) × (+3)
2 groups of +3 → 3 yellow chips in each group → total 6 yellow chips.
✅ Answer: +6
✏️ Example 2: (+2) × (–3)
2 groups of –3 → 3 red chips in each group → total 6 red chips.
✅ Answer: –6
✏️ Example 3: (–2) × (+3)
Think: “The opposite of 2 groups of +3.”
→ 2 groups of 3 yellow chips would be +6,
→ The opposite is –6 (red chips).
✅ Answer: –6
✏️ Example 4: (–2) × (–3)
Think: “The opposite of 2 groups of –3.”
→ 2 groups of red chips (–6),
→ The opposite of that is +6 (yellow chips).
✅ Answer: +6
📏 3. Number Line Model
Use repeated jumps to model multiplication:
Example: (+3) × (–2)
Start at 0 → make 3 jumps of –2 (each jump is left) → land on –6.
✅ Answer: –6
Example: (–3) × (–2)
Start at 0 → “the opposite of 3 jumps of –2” → move right → land on +6.
✅ Answer: +6
💡 Key Ideas
-
Multiplication is repeated addition or repeated subtraction.
-
Negative × Negative = Positive because taking “the opposite of an opposite” brings you back to positive.
Multiplying Integers Extra Worksheet
DIVIDING INTEGERS
➗ Dividing Integers (Using Signs Only)
When dividing integers, you use the same sign rules as for multiplication.
🧮 The Rules:
Sign PatternExampleResultExplanation
(+) ÷ (+)12 ÷ 3 = 4PositiveSame signs → positive
(–) ÷ (–)–12 ÷ –3 = 4PositiveSame signs → positive
(+) ÷ (–)12 ÷ –3 = –4NegativeDifferent signs → negative
(–) ÷ (+)–12 ÷ 3 = –4NegativeDifferent signs → negative
💡 Quick Rule to Remember
Same signs = Positive
Different signs = Negative
✏️ Examples
-
16 ÷ 4 = +4
-
–16 ÷ –4 = +4
-
16 ÷ –4 = –4
-
–16 ÷ 4 = –4
✅ Tip
When working with multiple steps (like in order of operations):
-
Simplify any signs first.
-
Then divide the numbers normally.
ORDER OF OPERATIONS
🔢 Order of Operations (Whole Numbers)
When solving math problems with more than one operation, you must follow a specific order so everyone gets the same answer!
🧮 The Rule: PEMDAS
💡 Say it like: “Please Excuse My Dear Aunt Sally”
Each letter stands for a step:
LetterStepExample
PParentheses first(3 + 2) × 4 = 20
EExponents next3² = 9
M/DMultiply or Divide (from left to right)8 ÷ 4 × 2 = 4
A/SAdd or Subtract (from left to right)10 – 3 + 2 = 9
✏️ Example 1:
8 + (5 × 2)
→ Do parentheses first: (5 × 2) = 10
→ Then add: 8 + 10 = 18 ✅
✏️ Example 2:
12 ÷ 3 + 4 × 2
→ Multiply and divide left to right:
12 ÷ 3 = 4 → 4 + 4 × 2
→ Then multiply: 4 × 2 = 8
→ Add: 4 + 8 = 12 ✅
✏️ Example 3:
(6 + 4) × 3 – 5
→ Parentheses: (6 + 4) = 10
→ Multiply: 10 × 3 = 30
→ Subtract: 30 – 5 = 25 ✅
💡 Tips
-
Always work left to right for multiplication/division and addition/subtraction.
-
Use brackets to make your meaning clear.
-
Check your work with estimation to see if it makes sense.
What is Order of Operations?
Order of operations with Exponents Video
ORDER OF OPERATIONS WITH NEGATIVE INTEGERS
🔢 Order of Operations with Negative Integers
When negatives appear in a problem, you still follow the same PEMDAS rule, but you must pay close attention to the negative signs (especially those in parentheses!).
🧮 The Rule: PEMDAS
P – Parentheses
E – Exponents
M/D – Multiply or Divide (from left to right)
A/S – Add or Subtract (from left to right)
⚠️ Be Careful With Negative Signs
-
If a negative number is in parentheses, it stays attached to that number.
Example: (–3) × 4 = –12 -
If there’s a minus sign outside parentheses, treat it like subtracting a negative.
✏️ Example 1:
(–3 + 5) × 2
1️⃣ Parentheses first → (–3 + 5) = 2
2️⃣ Multiply → 2 × 2 = 4 ✅
✏️ Example 2:
–4 + (–3 × 2)
1️⃣ Parentheses → (–3 × 2) = –6
2️⃣ Add → –4 + (–6) = –10 ✅
✏️ Example 3:
(–8 ÷ 4) + 6 × (–2)
1️⃣ Parentheses: (–8 ÷ 4) = –2
2️⃣ Multiply: 6 × (–2) = –12
3️⃣ Add: –2 + (–12) = –14 ✅
✏️ Example 4 (Exponents):
(–3)² + 5
→ (–3)² = (–3) × (–3) = 9
→ 9 + 5 = 14 ✅
🟥 Be careful!
Without parentheses: –3² = –9 (because exponent applies before the negative sign).
💡 Tips
-
Always use parentheses to make negatives clear.
-
Think of the negative sign as part of the number when multiplying or dividing.
-
Check with a calculator at the end to confirm your sign.